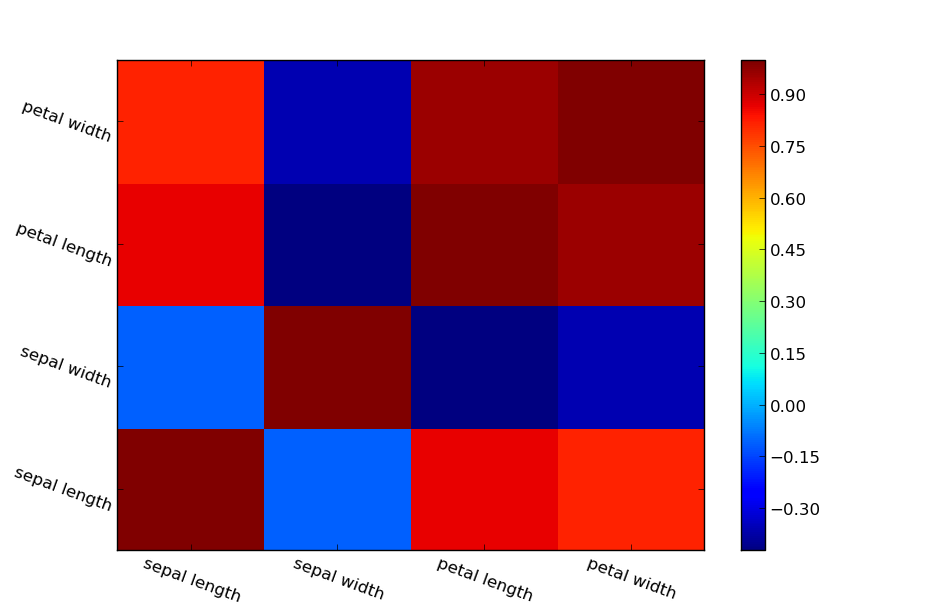
Classification is a data mining function that assigns samples in a dataset to target classes. The models that implement this function are called classifiers. There are two basic steps to using a classifier: training and classification. Training is the process of taking data that is known to belong to specified classes and creating a classifier on the basis of that known data. Classification is the process of taking a classifier built with such a training dataset and running it on unknown data to determine class membership for the unknown samples.
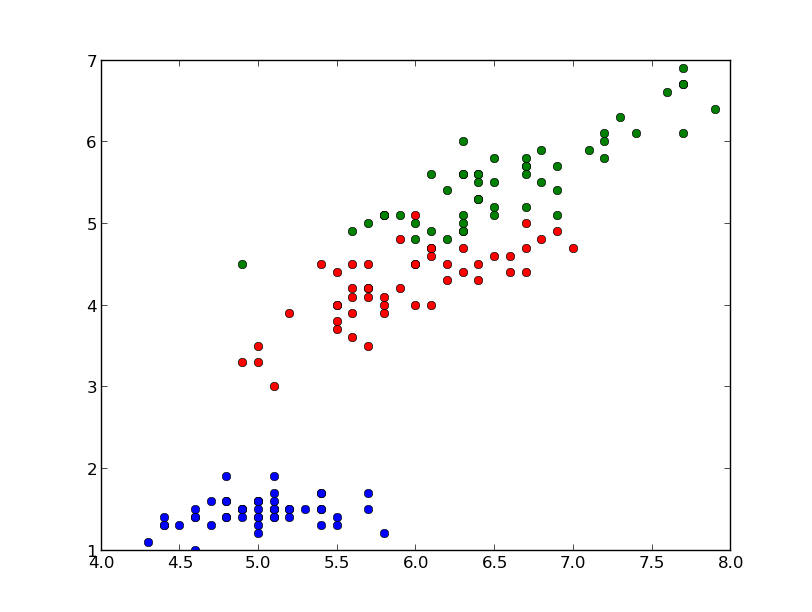
The library sklearn contains the implementation of many models for classification and in this section we will see how to use the Gaussian Naive Bayes in order to identify iris flowers as either setosa, versicolor or virginica using the dataset we loaded in the first section. To this end we convert the vector of strings that contain the class into integers:
Now we are ready to instantiate and train our classifier:
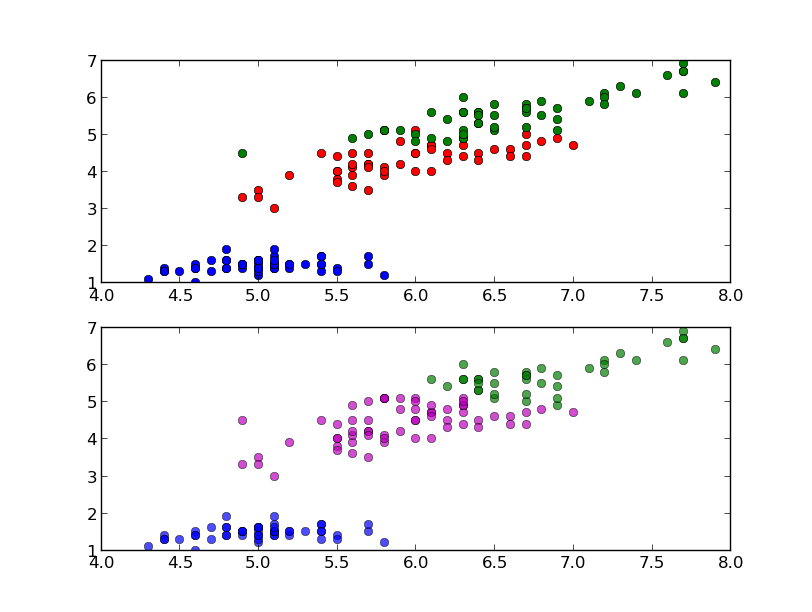
The classification can be done with the predict method and it is easy to test it with one of the sample:
In this case the predicted class is equal to the correct one (setosa), but it is important to evaluate the classifier on a wider range of samples and to test it with data not used in the training process. To this end we split the data into train set and test set, picking samples at random from the original dataset. We will use the first set to train the classifier and the second one to test the classifier. The function train_test_split can do this for us:
The dataset have been split and the size of the test is 40% of the size of the original as specified with the parameter test_size. With this data we can again train the classifier and print its accuracy:
In this case we have 93% accuracy. The accuracy of a classifier is given by the number of correctly classified samples divided by the total number of samples classified. In other words, it means that it is the proportion of the total number of predictions that were correct.
Another tool to estimate the performance of a classifier is the confusion matrix. In this matrix each column represents the instances in a predicted class, while each row represents the instances in an actual class. Using the module metrics it is pretty easy to compute and print the matrix:
In this confusion matrix we can see that all the Iris setosa and virginica flowers were classified correctly but, of the 26 actual Iris versicolor flowers, the system predicted that three were virginica. If we keep in mind that all the correct guesses are located in the diagonal of the table, it is easy to visually inspect the table for errors, since they are represented by the non-zero values outside of the diagonal.
A function that gives us a complete report on the performance of the classifier is also available:
Here is a summary of the measures used by the report:
- Precision: the proportion of the predicted positive cases that were correct
- Recall (or also true positive rate): the proportion of positive cases that were correctly identified
- F1-Score: the harmonic mean of precision and recall
The support is just the number of elements of the given class used for the test. However, splitting the data, we reduce the number of samples that can be used for the training, and the results of the evaluation may depend on a particular random choice for the pair (train set, test set). To actually evaluate a classifier and compare it with other ones, we have to use a more sophisticated evaluation model like Cross Validation. The idea behind the model is simple: the data is split into train and test sets several consecutive times and the averaged value of the prediction scores obtained with the different sets is the evaluation of the classifier. This time, sklearn provides us a function to run the model:
As we can see, the output of this implementation is a vector that contains the accuracy obtained with each iteration of the model. We can easily compute the mean accuracy as follows: